Domain And Range Negative And Positive Infinity

A problem that uses infinity in it s domain and range.

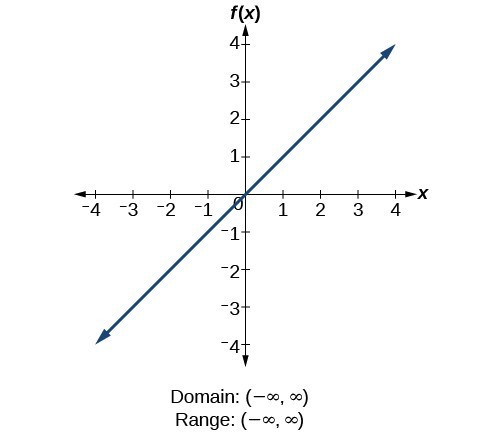
Domain and range negative and positive infinity. Hence every given domain value has one and only. For f x x 2 the domain in interval notation is. But for any real number whose square results in a positive number. As such it is not uncommon to say that a domain or range is from negative infinity to positive infinity.

In taking both domain and range into account a function is any mathematical formula that produces one and only one result for each input. But if your function is y x 2 your domain is still the set of real numbers. Consider a line such as f x 3x. When using interval notation domain and range are written as intervals of values.

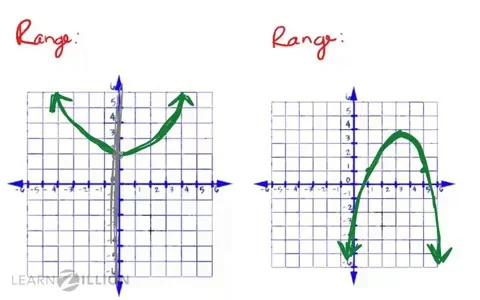
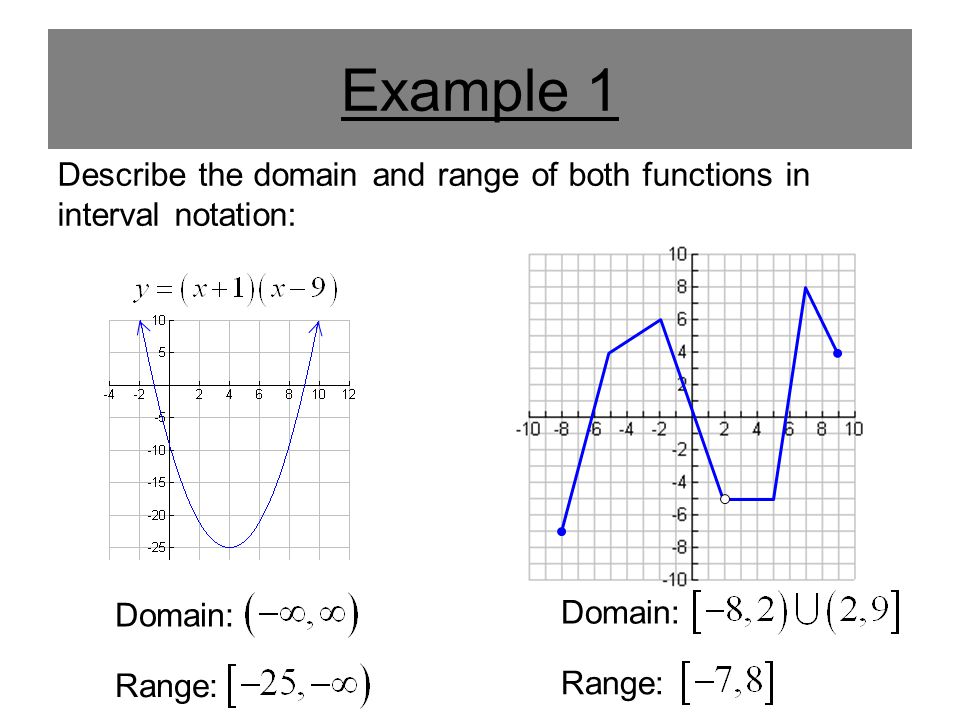
Our final domain for this function is infinity 2 because negative infinity cannot be obtained and 2 is obtained because of the closed dot. Therefore both positive and negative infinity will always use parenthesis. From the above graph you can see that the range for x 2 green and 4x 2 25 red graph is positive. Negative infinity on both sides or one side can go to negative infinity and the other towards positive infinity.

Make a table of values on your graphing calculator see. You could substitute values into x such as 13848 4892 38577 or 10000000000 and then calculate the corresponding y. Remember that infinity and negative infinity are not obtainable. You can take a good guess at this point that it is the set of all positive real numbers based on looking at the graph.

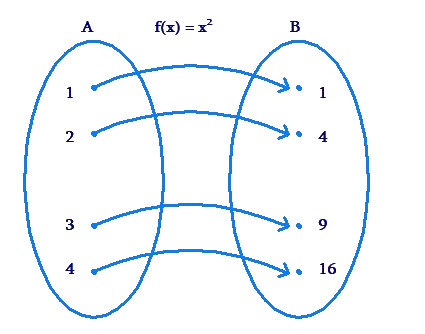
A problem that uses infinity in it s domain and range. Find the domain and range of a function with a table of values. For instance the function latex f x x 2 latex has a range of latex f x geq0 latex because the square of a number always yields a positive result. Here we have an arrow going onto negative infinity.

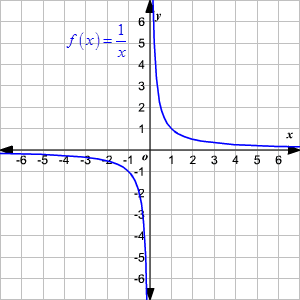
D indicates that you are talking about the domain and read as negative infinity to positive infinity is another way of saying that the domain is all real numbers. Graph of y 1 x which tends towards both negative and positive infinity at x 0.