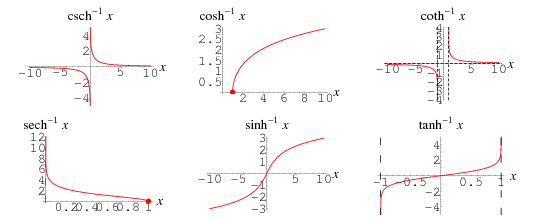
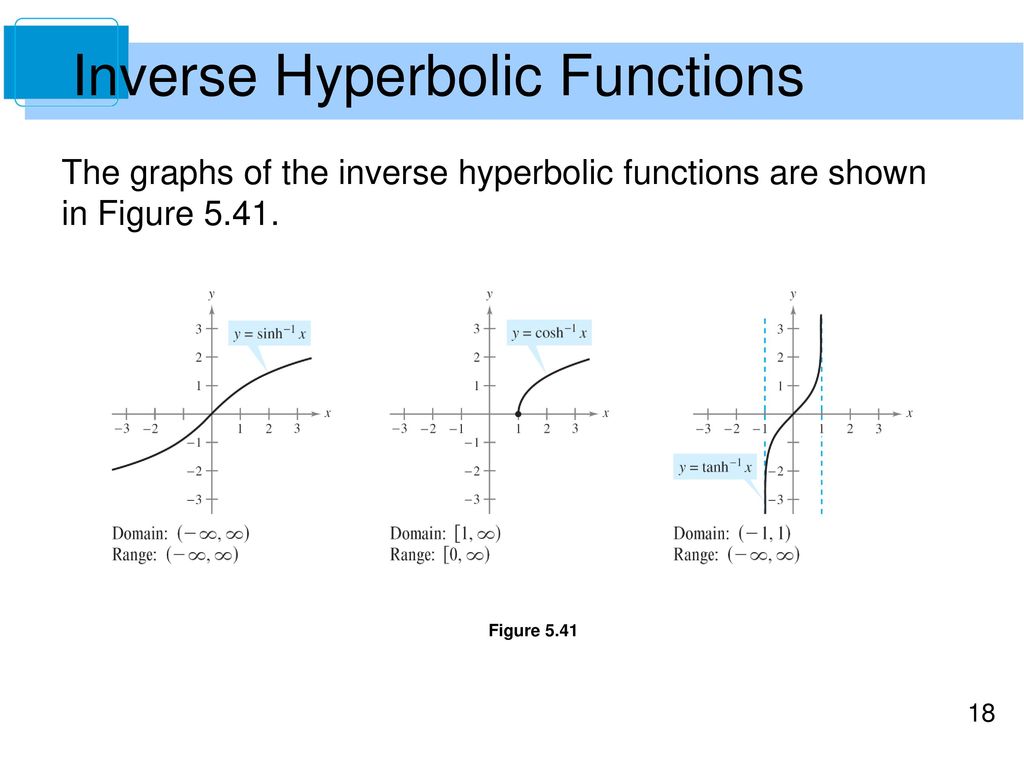
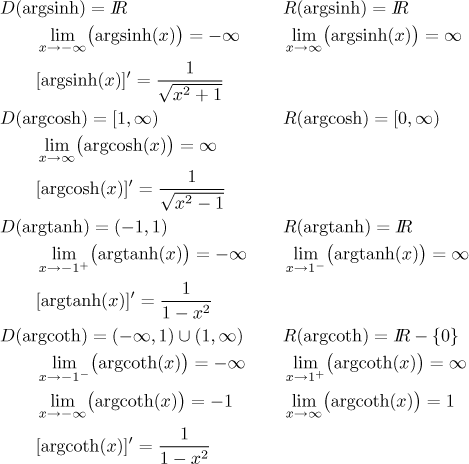Domain And Range Of Inverse Hyperbolic Functions

For complex arguments the inverse hyperbolic functions the square root and the logarithm are multi valued functions and the equalities of the next subsections may be viewed as equalities of multi valued functions.

Domain and range of inverse hyperbolic functions. Also a step by step calculator to find domain of a function and a step by step calculator to find range of a function are included in this website. Let so so e y e y 2x. The other hyperbolic functions have no inflection points. The graph of the inverse sine the reflection of the restricted sine in the liney x is shown in figure 2.

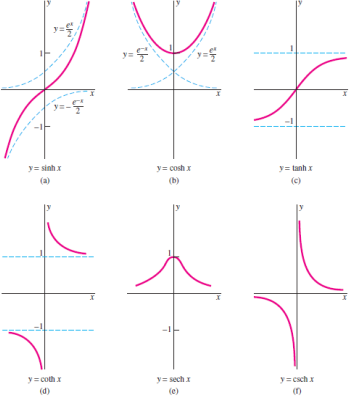
The inverse hyperbolic functions sometimes also called the area hyperbolic functions spanier and oldham 1987 p. Put z e y. A table of domain and range of common and useful functions is presented. In this unit we define the three main hyperbolic functions and sketch their graphs.

They are denoted cosh 1 z coth 1 z csch 1 z sech 1 z sinh 1 z and tanh 1 z. We may compute the derivatives of these functions as we have other inverse functions. The other hyperbolic functions have inverses as well though arcsech x is only a partial inverse. Table of domain and range of common functions.

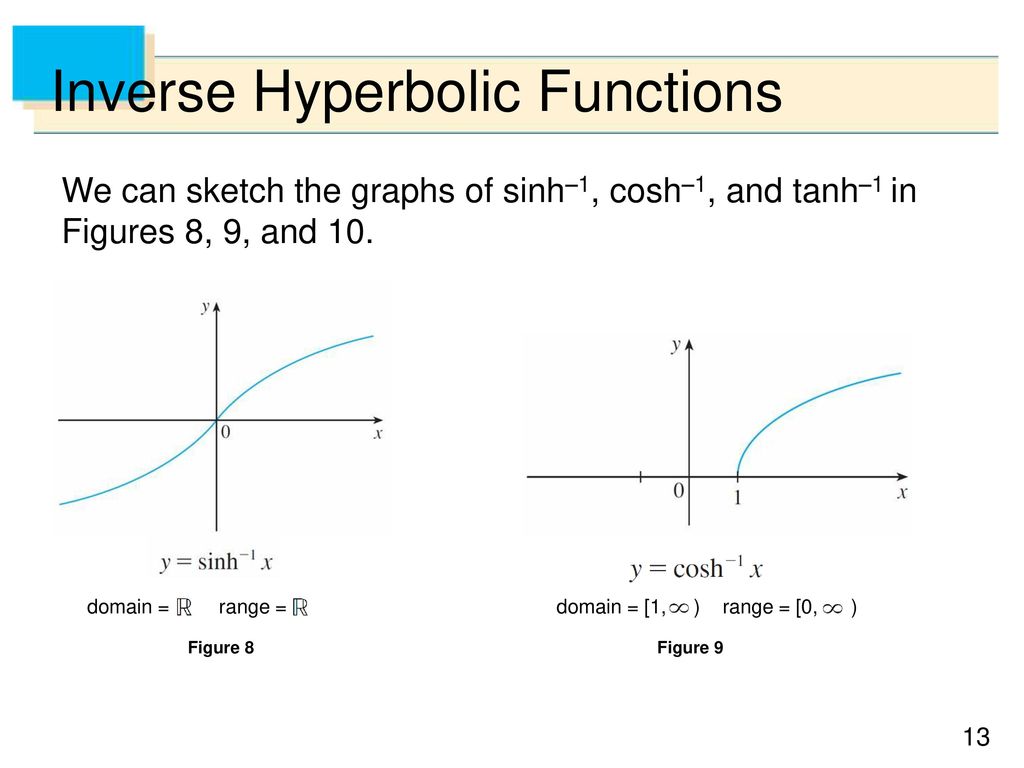
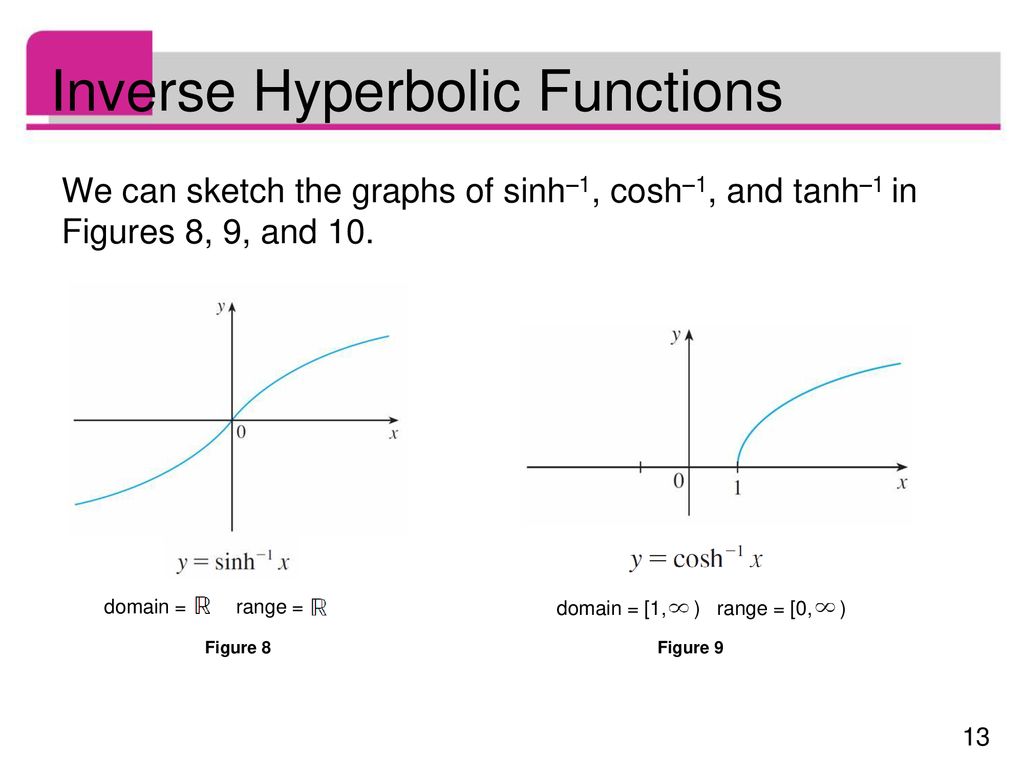
The inverse sine function is given by y sin 1 x x sin y π 2 y π 2 it is defined for 1 x 1 while its range the domain of the restricted sine is π 2 π 2. 263 are the multivalued function that are the inverse functions of the hyperbolic functions. We can get a formula for this function as follows. Here you will learn how to draw the inverse hyperbolic graphs arsinh x arcosh x artanh x arsech x arcosech x and arcoth x.

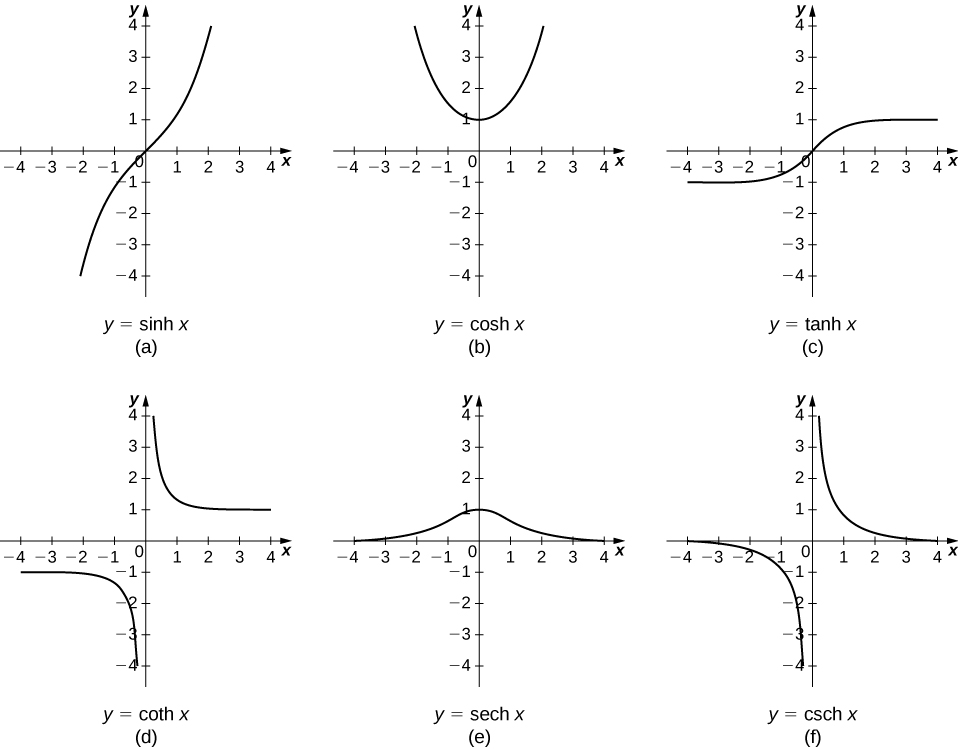
Hyperbolic functions the hyperbolic functions have similar names to the trigonmetric functions but they are defined in terms of the exponential function. For all inverse hyperbolic functions save the inverse hyperbolic cotangent and the inverse hyperbolic cosecant the domain of. Theorem 4 11 6 ds d over dx arcsinh x 1 over sqrt 1 x 2. Variants of these notations beginning with a capital letter are commonly used to denote their.

The hyperbolic sine function sinh x is one to one and therefore has a well defined inverse sinh 1 x shown in blue in the figure in order to invert the hyperbolic cosine function however we need as with square root to restrict its domain. We also discuss some identities relating these functions and mention their inverse functions and. Then so z 2 1 2xz so z 2 2xz 1 0. Similarly we define the other inverse hyperbolic functions.

If x sinh y then y sinh 1 a is called the inverse hyperbolic sine of x.