Domain Math Simply Connected

A topological space x is called simply connected if it is path connected and any loop in x defined by f.

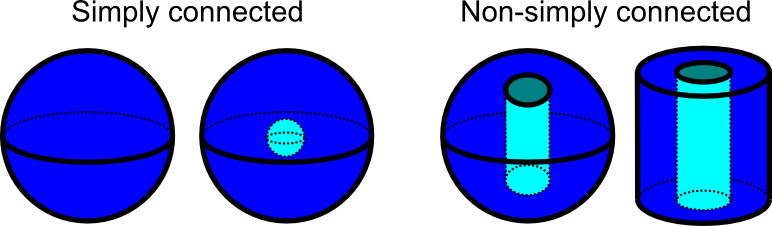
Domain math simply connected. A simply connected domain is one without holes going all the way through it. S 1 x can be contracted to a point. 55 xx the term refers often to open subsets omega which usually are assumed to be connected of the euclidean space mathbb r n where each closed path is homotopic to zero a closed path namely a. There exists a continuous map f.

Jenkins in handbook of complex analysis 20026 boundary correspondence. D 2 x such that f restricted to s 1 is f here s 1 and d 2 denotes the unit circle and closed unit disk in the euclidean plane respectively. 2010 mathematics subject classification. If the domain is connected but not simply it is said to be multiply connected in.

Simply connected a pathwise connected domain is said to be simply connected also called 1 connected if any simple closed curve can be shrunk to a point continuously in the set. By removing from such a domain d all the points of k 1 cuts that is jordan arcs joining pairs of connected components of the boundary it is always possible to obtain a simply connected domain d subset d. A simply connected domain δ of hyperbolic type on the sphere has two types of closure the ordinary point set closure and the closure obtained by adjoining its border given by regarding δ as a finite riemann surface. The domain dwill be an in nite.

The set e the two circles we re ect in and some of the other components of d. Learn mathematics create account or sign in connected and simply connected domains fold unfold table of contents connected and simply connected domains. In mathematical analysis a domain is any connected open subset of a finite dimensional vector space this is a different concept than the domain of a function though it is often used for that purpose for example in partial differential equations and sobolev spaces.