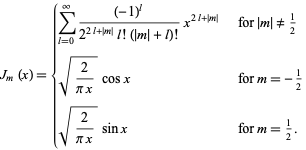Domain Of Bessel Function Order 1

Construction of a rst solution.

Domain of bessel function order 1. Bessel s equation of order α with α 0 is the second order differential equation 1 x2y xy x2 α2 y 0 in order to find all solutions we need two independent solutions. Is called bessel function of order 1. Find the domain of the bessel function of order 0 defined by let a n 1 n x 2n 2 2n n 2. Given the function f x 1 2 x x 2 2 x 3 k 0 a k x k where a 2 k 1 a 2 k 1 2 for any k 0 determine the domain of f and an explicit formula for it.

Although α and α produce the same differential equation it is conventional to define different bessel functions for these two values. Then thus by the ratio test the given series converges for all values of x. J ν x k 0 1 k x 2 ν 2k k γ ν k 1. J1 x 1 2n 1 n x n.

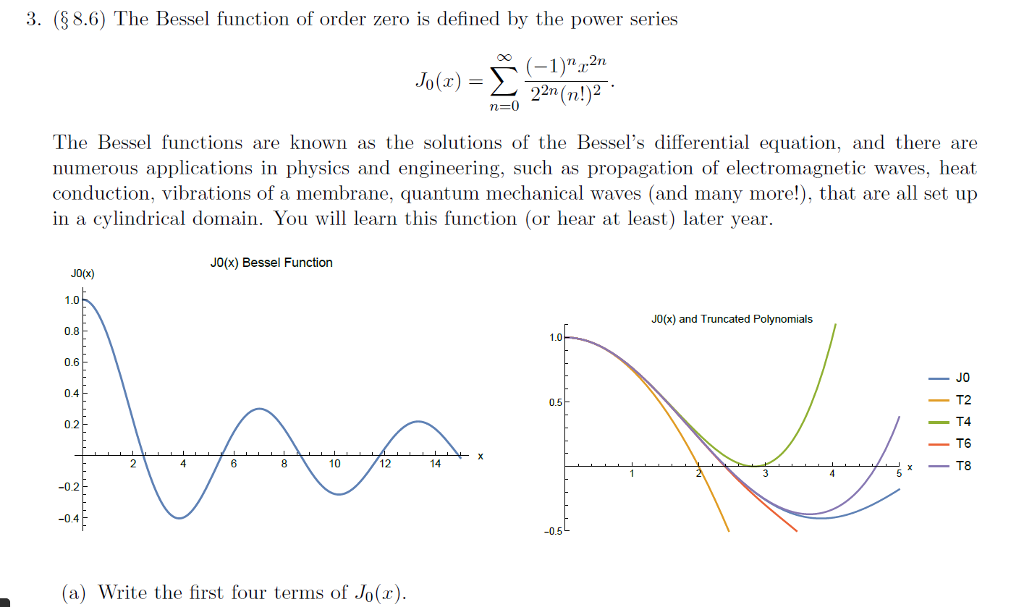
Bessel functions first defined by the mathematician daniel bernoulli and then generalized by friedrich bessel are canonical solutions y x of bessel s differential equation for an arbitrary complex number α the order of the bessel function. In other words the domain of the bessel function j 0 is infinity infinity r. Bessel functions of the second kind y ν x also known as weber or neumann func tions which are singular at x 0 the bessel function of the first kind of order ν can be be determined using an infinite power series expansion as follows. Bessel functions blue for integer orders 0 to 5 fig.

Note that x 0 is a singular point of the equation. First don t confuse bessel functions and modified bessel functions. Solved by expert tutors subscribe to unlock question find the domain of the bessel function of order 1. The zeroes of the functions can be seen in the crossing points of the graphs in gure 1 and gure 2.

More precisely it is a regular singular point. The modi ed bessel functions of the second kind for orders 0 to 5 4 and second kind have an in nite number of zeros as the value of xgoes to 1. The hankel transform of order of a function f r is given by where is the bessel function of the first kind of order with the inverse hankel transform of f ν k is defined as which can be readily verified using the orthogonality relationship described below. N 1.

Bessel functions of the first kind j ν x which are finite at x 0for all real values of ν 2. Inverting a hankel transform of a function f r is valid at every. Again different sub sets of functions. Attachment preview download attachment.

In one of each of whose two sets of functions they can be of the first kind or of the second kind. And in each one of these sub sets they are different bessel functions of various order.