Function Domain Empty Set

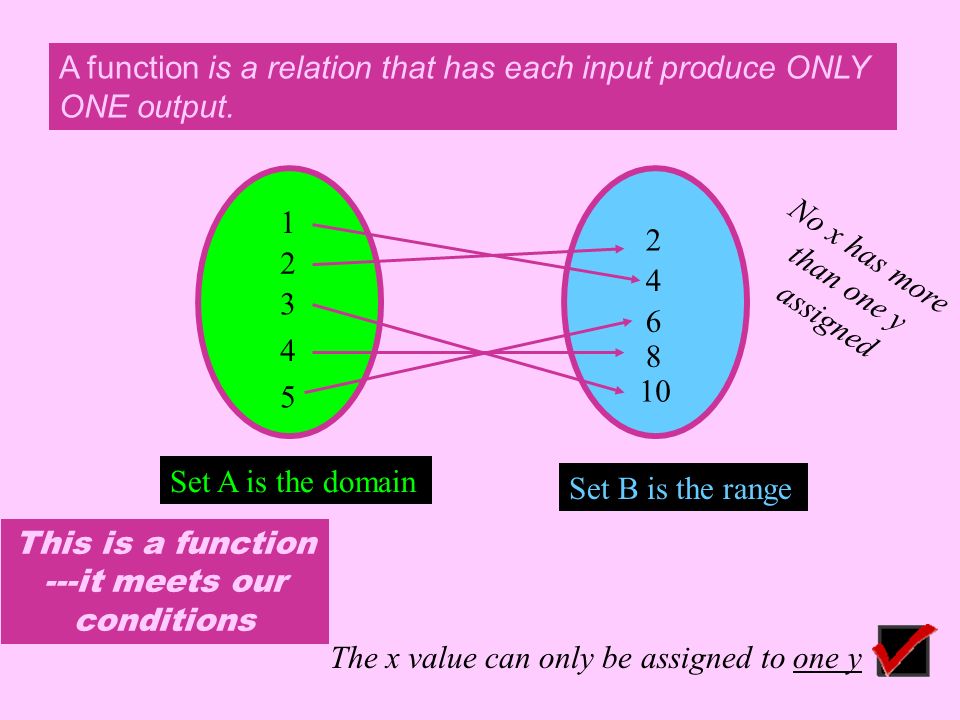
As a function table and as a set of coordinates.

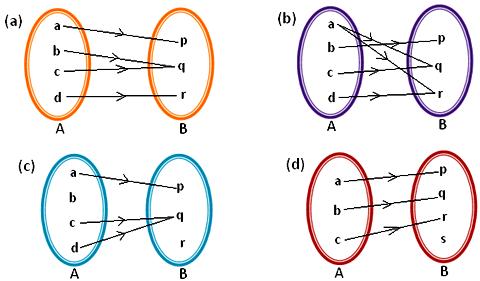
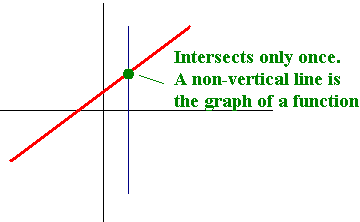
Function domain empty set. More generally every mathematical operation is defined as a multivariate function. The graph of an empty function is the empty set. For example a function like f x x has no real value for any real value of x its domain is an empty set. It is the set x in the notation f.

Stack exchange network consists of 176 q a communities including stack overflow the largest most trusted online community for developers to learn share their knowledge and build their careers. So according to this definition the answer would be no a function cannot have the empty set as the domain. The same is true for every binary operation. Given a set there exists exactly one function from the the empty set to that set.

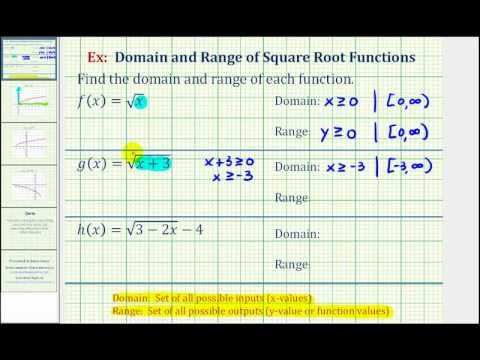
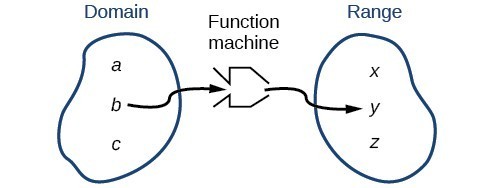
The domain and range of a function is all the possible values of the independent variable x for which y is defined. But if you remove that part of the definition i don t see any problems. X y and is alternatively denoted as displaystyle operatorname dom f. Sometimes it is useful to consider functionswhose domain is the empty set.

The range of a function is all the possible values of the dependent variable y. For example multiplication of integers is a function of two variables or bivariate function whose domain is the set of all pairs 2 tuples of integers and whose codomain is the set of integers. The example below shows two different ways that a function can be represented.