How To Find Domain And Range Of A Function Algebraically Pdf

It s ok if the numerator is zero we can divide into zero if we do we get zero but we are not allowed to divide by zero.

How to find domain and range of a function algebraically pdf. Set a is called the domain of the function f set b is the called the co domain of the function set of images of all elements in set a is called the range i e it is the set of values of f x which we get for each and every x in the domain. Example sketch the graph of f x 3x x2 and find a. Then plug that answer into the function to find the range. The range of f x 2 x 1 is 2.

The plot of a function f is shown below. Zeros of the denominator from the domain. Let f x be a real valued function. Thus the domain of the function is left 2 3 right also the variation in the function output is in the continuous interval from 1.

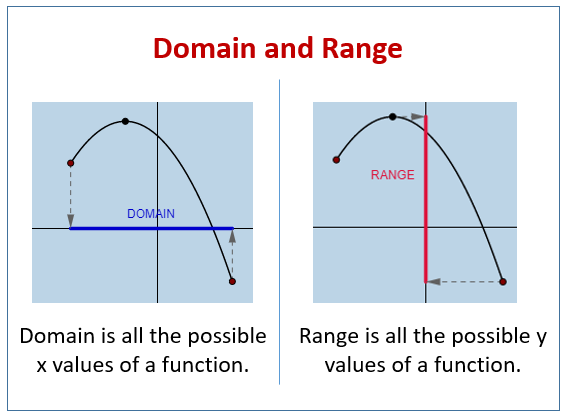
Then the domain of a function is the set of all possible values of x for which f x is defined. Energy information administration solution. How to find. How to find the domain of a function.

To properly notate the range write out the numbers in brackets if they re included in the domain or in parenthesis if they re not included in the domain. We observe that the graph corresponds to a continuous set of input values from 2 to 3. Find the domain and range of this function. Let y f x be a function with an independent variable x and a dependent variable y.

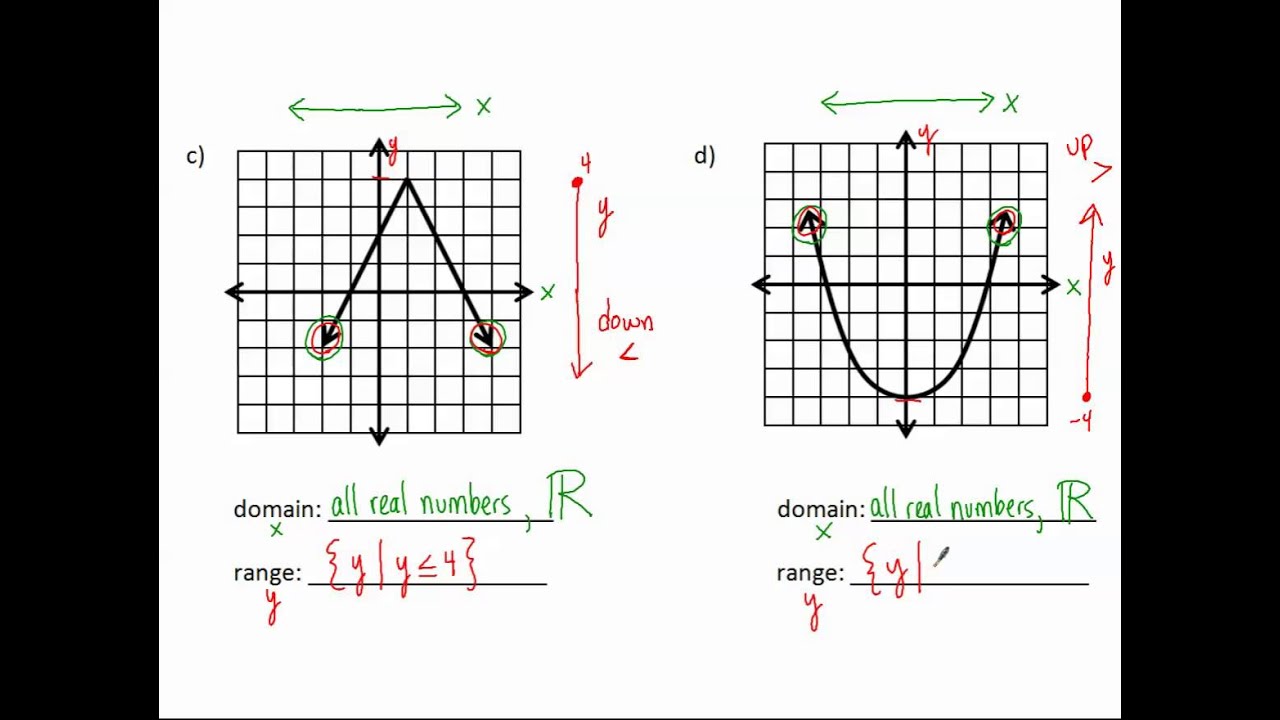
Find the domain and range of the function. First we learn what is the domain before learning how to find the domain of a function algebraically what is the domain of a function. Solution the domain of this parabola is all real x. Find the domain and range of the function latex f latex whose graph is shown in figure 9.

To find the range of a function first find the x value and y value of the vertex using the formula x b 2a. If a function f provides a way to successfully produce a single value y using for that purpose a value for x then that chosen x value is said to belong to the domain of f. Now lets see how to find the range of a function algebraically i e without plotting the graph. To see that we observe that the natural domain of this function is 1 since we request that the expression from which we extract the square root is non.

A function is expressed as. Eliminate these values from the domain. The range is all real y 3. 9 range of a function definition.

The input quantity along the horizontal axis is years which we represent with the variable latex t latex for time. The range of a function f consists of all values f x it assumes when x ranges over its domain. Example 1 find the domain of the function f x 2 x x2 4x 21. Y f x where x is the independent variable and y is the dependent variable.