Integral Domain Zero Function

If x i is nonzero we show that the set x i d x.

Integral domain zero function. F x x3 4x2 7x 10. Integral domains as always in this course a ring ris understood to be a commutative ring with unity. X n be a finite integral domain with x 0 as 0 and x 1 as 1. 7 3 integral and rational zeros of polynomials integral zeros theorem.

In the ring z 6 we have 2 3 0 and so 2 and 3 are zero divisors. Let d x 0 x 1 x 2. Math a2a math integrating a function over an interval where the line of symmetry is equidistant from the extreme values of the interval i e the line of symmetry begin the midpoint can yield zero. In z 6z 0 2 3 hence both 2 and 3 are divisors of zero.

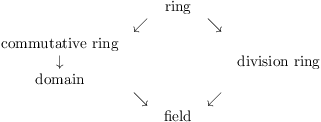
An integral domain is a commutative ring with an identity 1 0. Thus for example 0 is always a zero divisor. Integral domains and fields. In that case the function is odd or antisy.

A divisor of zero or zero divisor in ris an element r2r such that there exists an s2rwith s6 0 and rs 0. An integral domain is a nonzero commutative ring in which for every nonzero element r the function that maps each element x of the ring to the product xr is injective. An integral domain is a ring for which the set of nonzero elements is a commutative monoid under multiplication because a monoid must be closed under multiplication. These are two special kinds of ring definition.

A finite integral domain is a field. 1 first de nitions and properties de nition 1 1. If an integer a is a zero of a polynomial function with integral coefficients and a leading coefficient of 1 then a is a factor of the constant term of the polynomial. More generally if n is not prime then z n contains zero divisors.

Rings integral domains and fields 1 3 theorem 1 2 2. We start with giving the definition of the characteristic of a ring. Here the first argument is the expression the second is the variable to integrate over the third and fourth arguments are the limits of the integration and the optional fifth argument is the relative tolerance of the integral which must be between 0. We have to show that every nonzero element of d has a multiplicative inverse.

At the lower bound as x goes to 0 the function goes to and the upper bound is itself though the function goes to 0 thus this is a doubly improper integral. We prove that the characteristic of an integral domain is either 0 or a prime number. Consider for example the function 1 x 1 x integrated from 0 to shown right. Sometimes integrals may have two singularities where they are improper.

Let rbe a ring. If a b are two ring elements with a b 0 but ab 0 then a and b are called zero divisors.