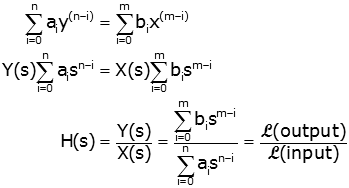Z Domain Transfer Function To Difference Equation

I have a z domain transfer function for a discrete time system i want to convert it into the impulse response difference equation form.

Z domain transfer function to difference equation. Often we will denote it h z. In matlab notation as indexes must start from 1 if we. The qi s are the roots of the equation n z 0 and are called the system zeros. It shows how signals flows in the system and the operations being performed on the signals.

The need for. Transfer functions in the z domain a very important category of lti systems is described by difference equations of the following type 00 nm kk kk aynk bxnk from which through z transform we obtain 0 0 m k k k n k k k bz hz az and 1 01 1 01 m m n n bbz bz yz x z aaz az where h z is the transfer function of the system. Answers 1 honglei chen on 27 jun 2012. The di erence equation p r y q r x with initial conditions x n 0 and y n 0 for n 0 called rest initial conditions satis es y q z 1 p z 1 x.

I am working on a signal processor. 3 as transfer function in z domain this is similar to the transfer function for. Link direct. In case the system is defined with a difference equation we could first calculate the impulse response and then calculating the z transform.

Z transform of difference equations since z transforming the convolution representation for digital filters was so fruitful let s apply it now to the general difference equation eq. Thus with rest ic y z x z h z. The filter order equals the number of poles or zeros in the transfer function whichever is greater. As an example consider the following difference equation.

Show hide all comments. System or transfer function theorem. Sign in to comment. Using the formula for the z transform of rwe get 1 8z 1 7z 2 y 1 z x.

Sign in to answer this question. 2 as difference equation this relates input sample sequence to output sample sequence. We call q z 1 p z 1 the system function. H z y z x z.

But it is far easier to calculate the z transform of both sides of the difference equation. To do this requires two properties of the z transform linearity easy to show and the shift theorem derived in 6 3 above. Please help me how to do it are there any direct functions. The pi s are the roots of the equation d z 0 and are defined as the system poles.

Y n 1 5y n 1 0 5y n 2 0 5x n remember that. If x n is the input of your discrete time system and y n is the output then the transfer fucntion h z is written as.