Domain Of Hyperbolic Function

Hyperbolic functions using osborn s rule which states that cos should be converted into cosh and sin into sinh except when there is a product of two sines when a sign change must be effected. For example cos2 x 1 2sin2 x can be converted remembering that sin 2 x sin x sin x into cosh2x 1 2sinh2 x. With appropriate range restrictions the hyperbolic functions all have inverses.

raise forest domain functional level order powershell join domain nano server qnap domain group permissions public domain journalism definition powershell join domain with new computer name raise domain functional level or forest first remove domain details windows 7 public domain free clip art christmas

$Math Tutor Functions Theory Elementary Functions$

Math Tutor Functions Theory Elementary Functions

Inverse Hyperbolic Functions From Wolfram Mathworld

$6 9 Calculus Of The Hyperbolic Functions Mathematics Libretexts$

6 9 Calculus Of The Hyperbolic Functions Mathematics Libretexts

What Is Hyperbolic Function A Plus Topper

5 Logarithmic Exponential And Other Transcendental Functions Ppt Download

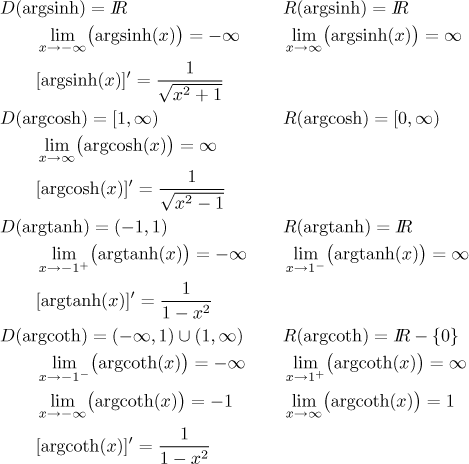
Answered What Are The Six Basic Hyperbolic Bartleby

$Answered What Are The Six Basic Hyperbolic Bartleby$

But sin2a 2sin acos a simply converts to sinh2a 2sinh a cosh a because there is no.

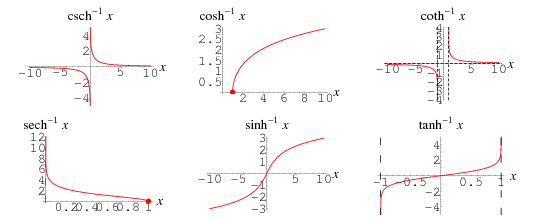
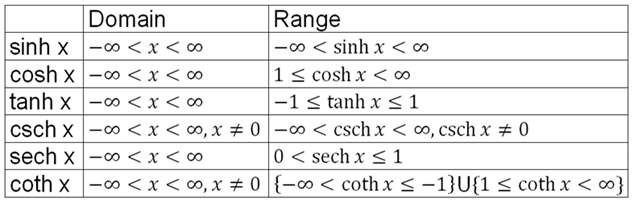
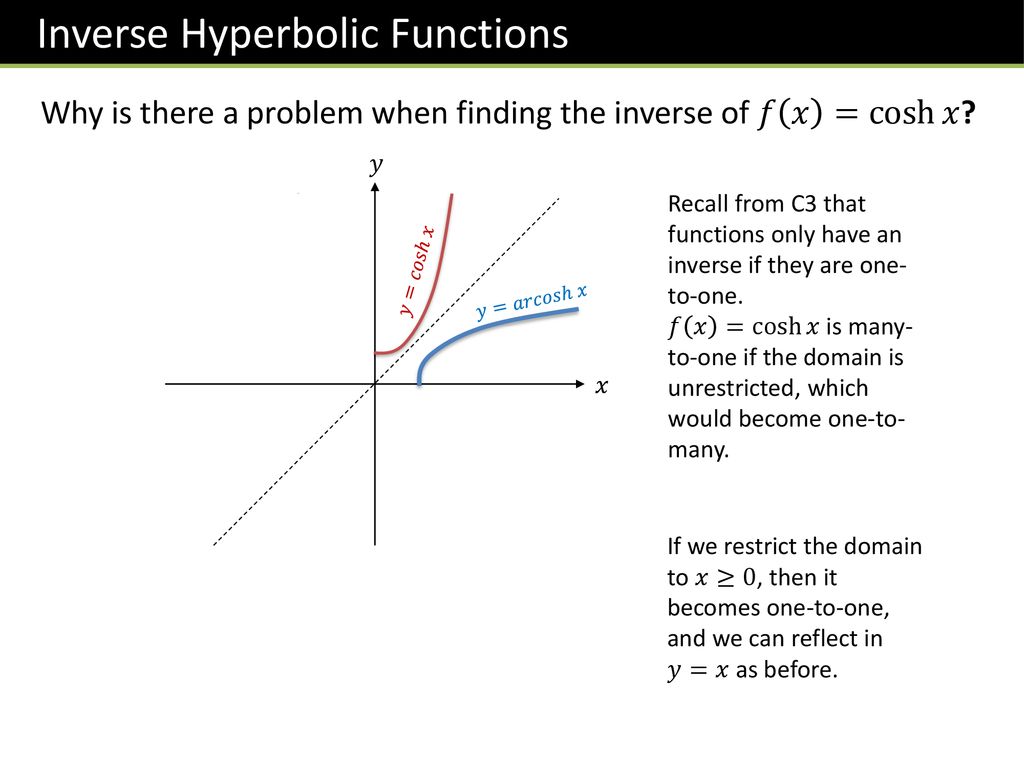
Domain of hyperbolic function. The inverse hyperbolic functions are multiple valued and as in the case of inverse trigonometric functions we restrict ourselves to principal values for which they can be considered as single valued. Similarly we define the other inverse hyperbolic functions. This is a bit surprising given our initial definitions. Ify their domains deﬁne the reprocal functions sechx cschx and cothx.

Other related functions 9 1 c mathcentre january 9 2006. Which is a single valued analytic function which coincides with one specific branch of the multivalued function over a domain consisting of the complex plane in which a finite number of arcs usually half lines or line segments have been removed. In complex analysis the hyperbolic functions arise as the imaginary parts of sine and cosine. Most of the necessary range restrictions can be discerned by close examination of the graphs.

These arcs are called branch cuts. These differentiation formulas give rise in turn to integration formulas. The hyperbolic functions take a real argument called a hyperbolic angle the size of a hyperbolic angle is twice the area of its hyperbolic sector the hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector. In this lesson we ll learn how to draw graphs of hyperbolic functions.

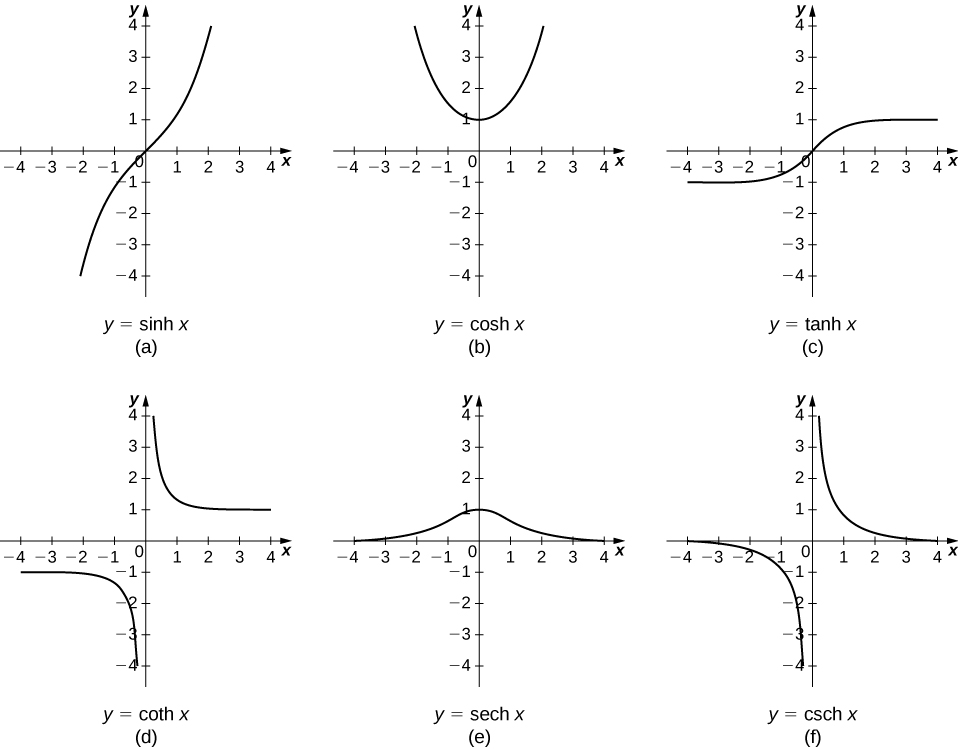
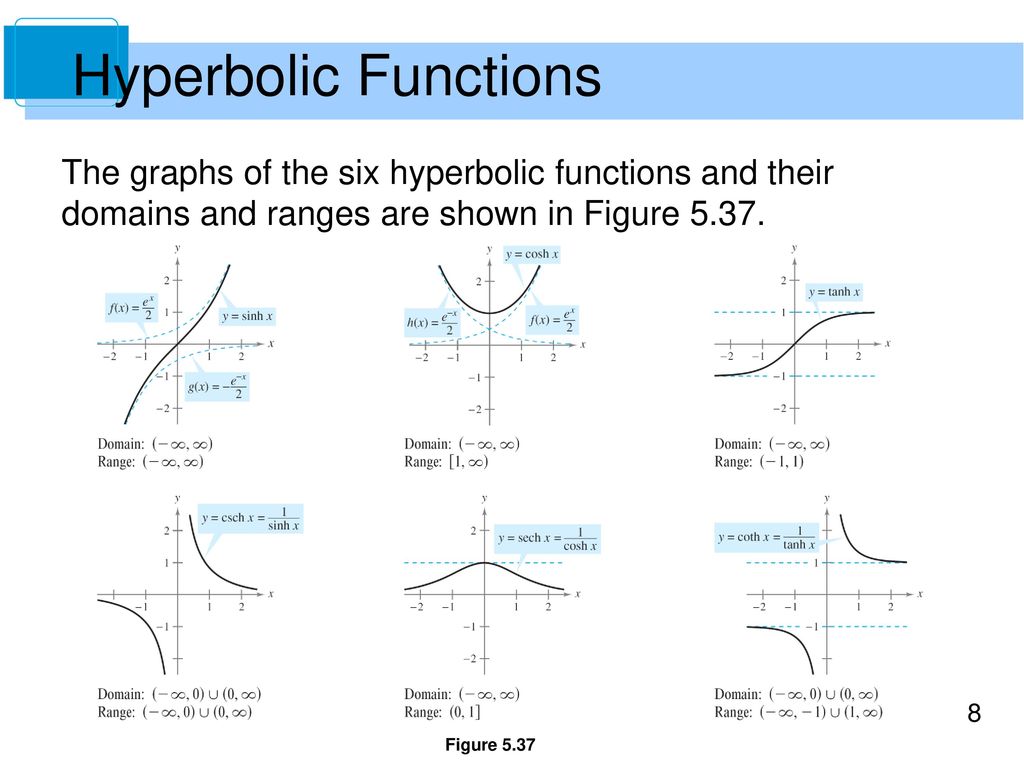
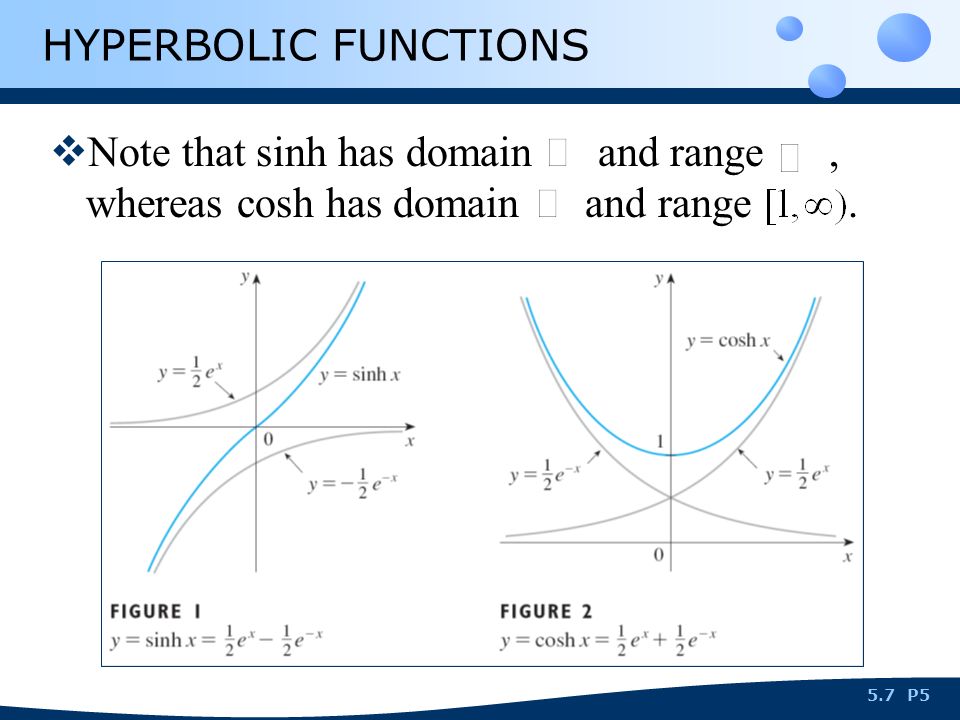
Deﬁning f x sinhx 4 4. Hyperbolic functions are defined in terms of exponential functions. Looking at the graphs of the hyperbolic functions we see that with appropriate range restrictions they all have inverses. Definition 4 11 1 the hyperbolic cosine is the function cosh x e x e x over2 and the hyperbolic sine is the function sinh x e x e x over 2 notice that cosh is even that.

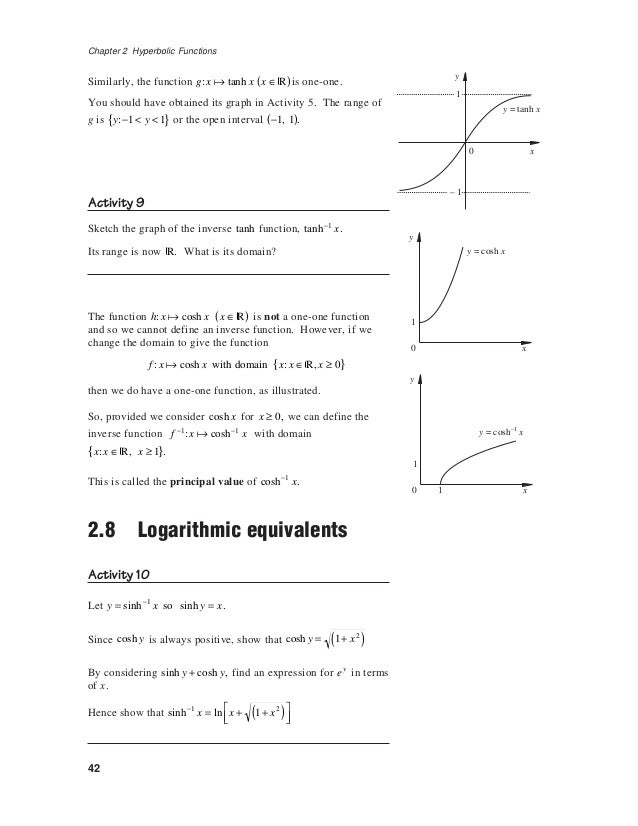
Deﬁning f x tanhx 7 5. Introduction in this video we shall deﬁne the three hyperbolic functions f x sinhx f x coshx. Identities for hyperbolic functions 8 6. Hyperbolic functions occurs in the calculations of angles and distances in hyperbolic geometry.

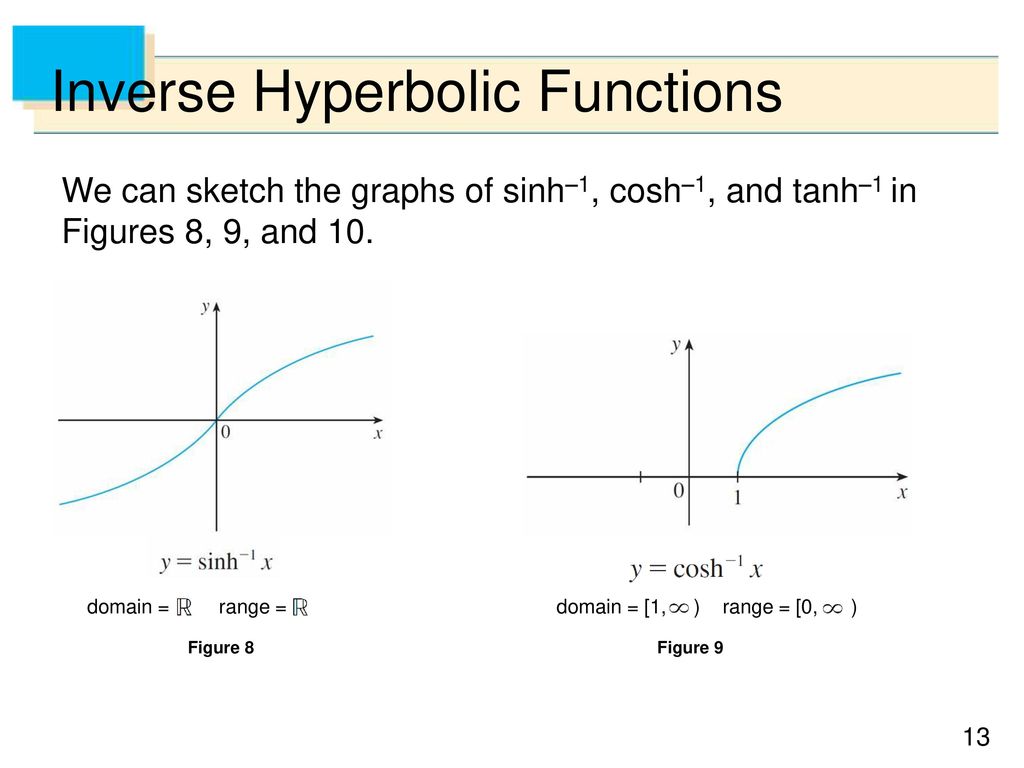
Deﬁning f x coshx 2 3. The hyperbolic functions appear with some frequency in applications and are quite similar in many respects to the trigonometric functions. The domains and ranges of the inverse hyperbolic functions are summarized in the following table. Term by term differentiation yields differentiation formulas for the hyperbolic functions.

If x sinh y then y sinh 1 a is called the inverse hyperbolic sine of x.